Công thức 7 Hằng đẳng thức đáng nhớ đầy đủ, chính xác nhất – Pretty Woman đã tổng hợp thông tin từ nhiều nguồn, giúp bạn có góc nhìn đa chiều hơn. Nào chúng ta bắt đầu thôi
7 hằng đẳng thức đáng nhớ lớp 7, 8, 9 – công thức và bài tập.
/Toán/ 7 Hằng Đẳng Thức Đáng Nhớ Lớp 7, 8, 9 – Hệ Thức Và Bài Tập.
- 2. Tháng 11 năm 2022
- Người quản lý
- toán học
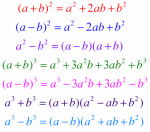
Trong chương trình THCS lớp 7, 8, 9, việc học thuộc lòng 7 hằng đẳng thức đáng nhớ là vô cùng quan trọng để học tốt môn Toán. Vì vậy, các em nhớ lặp lại liên tục hằng đẳng thức để áp dụng vào giải bài tập toán nhanh và chính xác nhất.
- bảng lượng giác
- Phương trình lượng giác trong tam giác
- Đặc điểm và dấu hiệu nhận biết hình thoi
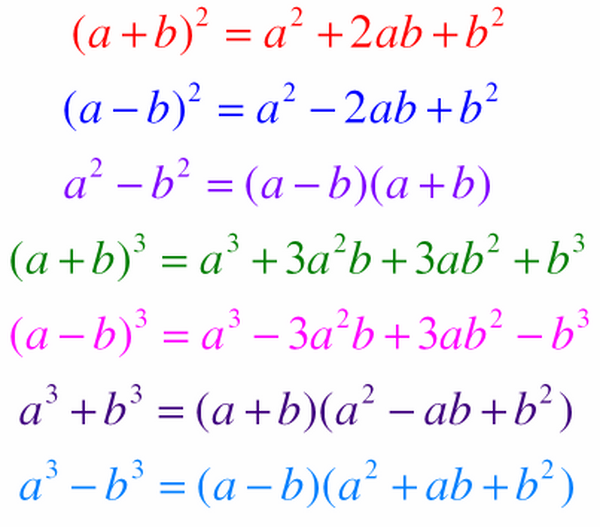
7 hằng đẳng thức đáng nhớ
Bình phương của một tổng : ( a + b )² = a² + 2ab + b²
Bình phương của một hiệu : ( a – b )² = a² – 2ab + b²
Hiệu hai bình phương : a² – b² = ( a + b ) (a – b )
Lập phương của một tổng : ( a + b )³ = a³ + 3a²b + 3ab² + b³
Lập phương của một hiệu : ( a – b )³ = a³ – 3a²b + 3ab² – b³
Tổng hai lập phương : a³ + b³ = ( a + b ) ( a² – ab + b² )
Hiệu hai lập phương : a³ – b³ = ( a – b ) ( a² + ab + b² )
Phát biểu bẩy hằng đẳng thức đáng nhớ bằng lời
- Bình phương của 1 tổng sẽ bằng bình phương của số thứ 1 cộng với hai lần tích của số thứ nhất với số thứ hai cộng bình phương số thứ hai
- Bình phương của 1 hiệu sẽ bằng bình phương của số thứ 1 trừ 2 lần tích số thứ nhất với số thứ 2 cộng với bình phương số thứ 2.
- Hiệu của 2 bình phương sẽ bằng tích của tổng 2 số với hiệu 2 số.
- Lập phương của 1 tổng sẽ bằng với lập phương số thứ 1 + 3 lần tích bình phương số thứ 1 với số thứ 2 + 3 lần tích số thứ 1 với bình phương số thứ 2 + lập phương số thứ 2.
- Lập phương của 1 tổng sẽ bằng với lập phương số thứ 1 -3 lần tích bình phương số thứ 1 với số thứ 2 + 3 lần tích số thứ 1 với bình phương số thứ 2 – lập phương số thứ 2.
- Tổng hai lập phương sẽ bằng tích giữa tổng 2 số với bình phương thiếu của 1 hiệu.
- Hiệu của 2 lập phương sẽ bằng với tích giữa hiệu hai số với bình phương thiếu của 1 tổng.
1. Bình phương của một tổng
(a + b)² = a² + 2ab + b²
- Bình phương của một tổng bằng bình phương của số thứ nhất cộng với hai lần tích của số thứ nhất nhân với số thứ hai, cộng với bình phương của số thứ hai
2. Bình phương của một hiệu
(a – b)² = a² – 2ab + b²
- Bình phương của một hiệu bằng bình phương của số thứ nhất trừ đi hai lần tích của số thứ nhất nhân số thứ hai sau đó cộng bình phương với số thứ hai.
3. Hiệu hai bình phương
a² – b² = (a – b)(a + b)
- Hiệu hai bình phương của hai số bằng tổng hai số đó nhân với hiệu hai số đó.
4. Lập phương của một tổng
(a + b)³ = A³ + 3a²b + 3ab² + b³
- Lập phương của một tổng hai số bằng lập phương của số thứ nhất cộng với ba lần tích bình phương số thứ nhất nhân số thứ hai cộng với ba lần tích số thứ nhất nhân với bình phương số thứ hai cộng với lập phương số thứ hai.
5. Lập phương của một hiệu
(a – b)³ = a³ – 3a²b + 3ab² – b³
- Lập phương của một hiệu hai số bằng lập phương của số thứ nhất trừ đi ba lần tích bình phương của số thứ nhất nhân với số thứ hai cộng với ba lần tích số thứ nhất nhân với bình phương số thứ hai trừ đi lập phương số thứ hai
6. Tổng hai lập phương
a³ + b³ = (a + b)(a² – ab + b² )
- Tổng của hai lập phương hai số bằng tổng của hai số đó nhân với bình phương thiếu của hiệu hai số đó
7. Hiệu hai lập phương
a³ – b³ = (a – b)(a² + ab + b²)
- Hiệu của hai lập phương của hai số bằng hiệu hai số đó nhân với bình phương thiếu của tổng của hai số đó.
Hằng đẳng thức mở rộng
Hằng đẳng thức đáng nhớ với hàm bậc 2
( a + b + c )² = a² + b² + c² + 2ab + 2ac + 2bc
( a + b – c )² = a² + b² + c² + 2ab – 2ac – 2bc
( a – b – c )² = a² + b² + c² – 2ab – 2ac + 2bc
Hằng đẳng thức đáng nhớ với hàm bậc 3
a³ + b³ = ( a + b )³ – 3ab( a + b)
a³ – b³ = ( a – b )³ + 3ab( a – b )
( a + b + c )³ = a³ + b³ + c³ + 3( a + b )( a + c )( b + c )
a³ + b³ + c³ – 3abc = ( a + b + c )( a² + b² + c² – ab – bc – ac )
( a – b )³ + ( b – c )³ + ( c – a )³ = 3( a – b )( b – c )( c – a )
( a + b )( b + c )( c + a ) – 8abc = a( b – c )² + b( c – a )² + c( a – b )²
( a + b )( b + c )( c + a ) = ( a + b + c ) ( ab + bc + ca ) – abc
Hằng đẳng thức dạng tổng quát .
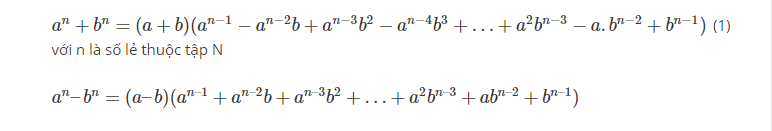
Các dạng bài tập về hằng đẳng thức đáng nhớ
Dạng 1: Tính giá trị của các biểu thức.
Dạng 2: Chứng minh biểu thức a mà không phụ thuộc biến.
Dạng 3: Áp dụng để tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức.
Dạng 4: Chứng minh đẳng thức bằng nhau.
Dạng 5: Chứng minh bất đẳng thức
Dạng 6: Phân tích đa thức thành nhân tử.
Dạng 7: Tìm giá trị của x
Bài tập về hằng đẳng thức đáng nhớ
bài tập 1 : Với a và b là hai số bất kì, thức hiện phép tính (a + b)(a + b).
đáp án
(a + b)(a + b) = a(a + b) + b(a + b)
= a2 + ab + ba + b2
= a2 + 2ab + b2
bài tập 2 : Tính [a + (-b)]2 (với a, b là các số tùy ý).
đáp án
Ta áp dụng hằng đẳng thức 1 ta có như sau
[ a + (-b)]² = a² + 2.a.(-b) + ( -b)² = a² – 2ab + b² .
Ví dụ 3: Tìm giá trị củ x biết: x2( x – 3) – 4x + 12 = 0
đáp án
x² (x – 3) – 4x + 12 = 0 ⇔ x² (x – 3) – 4(x – 3) = 0 ⇔ (x – 3) (x2 – 4) = 0 ⇔ (x – 3)(x – 2)(x + 2) = 0 ⇔ (x – 3) = 0 hoặc (x – 2) = 0 hoặc (x + 2) = 0 ⇔ x = 3 hoặc x = 2 hoặc x = –2 ⇒ Kết luận, vậy nghiệm : x = 3; x = 2; x = –2
Trên đây là toàn bộ kiến thức về 7 hằng đẳng thức đáng nhớ lớp 7,8,9 trong chương trình trung học cơ sở mà các bạn cần lắm được để áp dụng bẩy hằng đẳng thức đáng nhớ vào các dạng bài tập chi tiết nhất.
Bài viết liên quan
-
Bảng công thức lượng giác Sin Cos, cơ bản, nâng cao lớp 10,11 cần nhớ.
-
Nhân chia trước cộng trừ sau, quy tắc toán học lớp 2,3.
-
Bảng cửu chương nhân, chia 1,2,3,4,5,6,7,8,9,10 có hình ảnh.
-
Cách tính nhẩm cộng trừ nhanh lớp 2 – Mẹo cộng trừ nhanh bằng tay.
-
Tích phân từng phần, Bài tập tích phân từng phần
-
Tích phân suy rộng – Toán cao cấp. bierelarue
Trả lời Hủy
Email của bạn sẽ không được hiển thị công khai. Các trường bắt buộc được đánh dấu *
Bình luận
Tên *
Email *
Trang web
Home
>
Toán Học
>
7 Hằng Đẳng Thức Đáng Nhớ lớp 8 Chi Tiết, Đầy Đủ, Chính Xác
7 Hằng Đẳng Thức Đáng Nhớ lớp 8 Chi Tiết, Đầy Đủ, Chính Xác
7 hằng đẳng thức đáng nhớ là những hằng đẳng thức không còn xa lạ với các bạn nữa, Hôm nay THPT CHUYÊN LAM SƠN sẽ nói kỹ hơn về 7 hằng đẳng thức quan trọng là : bình phương của một tổng, bình phương của một hiệu, hiệu của hai bình phương, lập phương của một tổng, lập phương của một hiệu, tổng hai lập phương và cuối cùng là hiệu hai lập phương.
Nội Dung
- Chi tiết 7 hẳng đẳng thức đáng nhớ như sau
- 1. Bình phương của một tổng
- 2. Bình phương của một hiệu
- 3. Hiệu hai bình phương
- 4. Lập phương của một tổng
- 5. Lập phương của một hiệu
- 6. Tổng hai lập phương
- 7. Hiệu hai lập phương
- Hằng đẳng thức mở rộng
- Một số bài tập áp dụng bảy hằng đẳng thức đáng nhớ
Chi tiết 7 hẳng đẳng thức đáng nhớ như sau
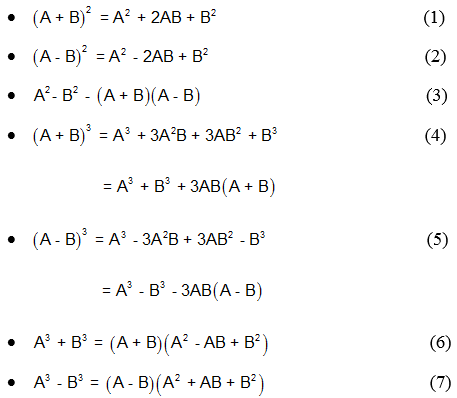
1. Bình phương của một tổng
=> Bình phương của một tổng sẽ bằng bình phương của số thứ nhất cộng hai lần tích của số thứ nhất và số thứ hai, sau đó cộng với bình phương của số thứ hai.
Ta có

2. Bình phương của một hiệu
=> Bình phương của một hiệu sẽ bằng bình phương của số thứ nhất trừ đi hai lần tích của số thứ nhất và số thứ hai, sau đó cộng với bình phương của số thứ hai.
Ta có

3. Hiệu hai bình phương
=> Hiệu của hai bình phương của hai số sẽ bằng hiệu của hai số đó nhân với tổng của hai số đó.
Ta có

4. Lập phương của một tổng
=> Lập phương của một tổng của hai số sẽ bằng lập phương của số thứ nhất cộng với ba lần tích của bình phương số thứ nhất nhân cho số thứ hai, cộng với ba lần tích của số thứ nhất nhân với bình phương của số thứ hai, rồi sau đó cộng với lập phương của số thứ hai.
Ta có

5. Lập phương của một hiệu
=> Lập phương của một hiệu của hai số sẽ bằng lập phương của số thứ nhất trừ đi ba lần tích của bình phương số thứ nhất nhân cho số thứ hai, cộng với ba lần tích của số thứ nhất nhân với bình phương của số thứ hai, rồi sau đó trừ đi lập phương của số thứ hai.
Ta có

6. Tổng hai lập phương
=> Tổng của hai lập phương của hai số sẽ bằng tổng của số thứ nhất cộng với số thứ hai, sau đó nhân với bình phương thiếu của tổng số thứ nhất và số thứ hai.
Ta có
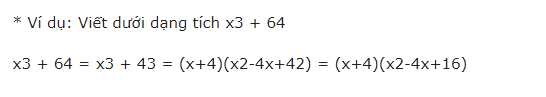
7. Hiệu hai lập phương
=> Hiệu của hai lập phương của hai số sẽ bằng hiệu của số thứ nhất trừ đi số thứ hai, sau đó nhân với bình phương thiếu của tổng số thứ nhất và số thứ hai.
Ta có
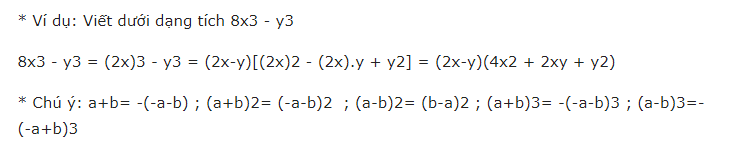
=> Đây là 7 đẳng thức này được sử dụng thường xuyên trong các bài toán liên quan đến giải phương trình, nhân chia các đa thức, biến đổi biểu thức tại cấp học trung học cơ sở và trung học phổ thông. Học thuộc bảy hằng đẳng thức đáng nhớ giúp giải nhanh những bài toán phân tích đa thức thành nhân tử.
Hằng đẳng thức mở rộng
Ngoài ra, người ta đã suy ra được các hằng đẳng thức mở rộng liên quan đến các hằng đẳng thức trên:
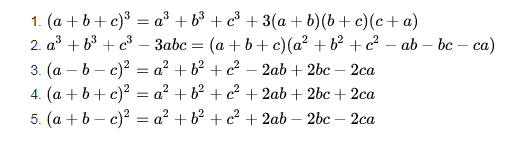
Đây là những hằng đẳng thức rất quan trọng chính vì vậy các em cần nhớ rõ trong đầu để mối khi làm bài tập về nhân chia các đa thức, biến đổi biểu thức tại cấp học trung học cơ sở và trung học phổ thông.
Một số bài tập áp dụng bảy hằng đẳng thức đáng nhớ
Dạng 1 : Tính giá trị của biểu thức
Ví dụ: Tính giá trị của biểu thức : A = x2 – 4x + 4 tại x = -1
* Lời giải.
– Ta có : A = x2 – 4x + 4 = x2 – 2.x.2 + 22 = (x – 2)2
– Tại x = -1 : A = ((-1) – 2)2=(-3)2= 9
⇒ Kết luận: Vậy tại x = -1 thì A = 9
Dạng 2 : Chứng minh biểu thức A không phụ thuộc vào biến
Ví dụ: Chứng minh biểu thức sau không phụ thuộc vào x: A = (x – 1)2 + (x + 1)(3 – x)
* Lời giải.
– Ta có: A =(x – 1)2 + (x + 1)(3 – x) = x2 – 2x + 1 – x2 + 3x + 3 – x = 4 : hằng số không phụ thuộc vào biến x.
Dạng 3 : Tìm giá trị nhỏ nhất của biểu thức
Ví dụ: Tính giá trị nhỏ nhất của biểu thức: A = x2 – 2x + 5
* Lời giải:
– Ta có : A = x2 – 2x + 5 = (x2 – 2x + 1) + 4 = (x – 1)2 + 4
– Vì (x – 1)2 ≥ 0 với mọi x.
⇒ (x – 1)2 + 4 ≥ 4 hay A ≥ 4
– Vậy giá trị nhỏ nhất của A = 4, Dấu “=” xảy ra khi : x – 1 = 0 hay x = 1
⇒ Kết luận GTNN của A là: Amin = 4 ⇔ x = 1
Dạng 4 : Tìm giá trị lớn nhất của biểu thức
Ví dụ: Tính giá trị lớn nhất của biểu thức: A = 4x – x2
* Lời giải:
– Ta có : A = 4x – x2 = 4 – 4 + 4x – x2 = 4 – (4 – 4x + x2) = 4 – (x2 – 4x + 4) = 4 – (x – 2)2
– Vì (x – 2)2 ≥ 0 với mọi x ⇔ -(x – 2)2 ≤ 0 với mọi x
⇔ 4 – (x – 2)2 ≤ 4 [cộng 2 vế với 4]
⇔ A ≤ 4 Dấu “=” xảy ra khi : x – 2 = 0 hay x = 2
⇒ Kết luận GTLN của A là: Amax = 4 ⇔ x = 2.
Dạng 5 : Chứng minh đẳng thức bằng nhau
Ví dụ: Chứng minh đẳng thức sau đúng: (a + b)3 – (a – b)3 = 2b(3a2 + b2)
* Lời giải:
– Đối với dạng toán này chúng ta biến đổi VT = VP hoặc VT = A và VP = A
– Ta có: VT = (a + b)3 – (a – b)3
= (a3 + 3a2b + 3ab2 + b3) – (a3 – 3a2b + 3ab2 – b3)
= a3 + 3a2b + 3ab2 + b3 – a3 + 3a2b – 3ab2 + b3
= 6a2b + 2b3
= 2b(3a2 + b2) = VP (đpcm).
⇒ Kết luận, vậy : (a + b)3 – (a – b)3 = 2b(3a2 + b2)

Dạng 7: Phân tích đa thức thành nhân tử
Ví dụ 1: Phân tích đa thức sau thành nhân tử: A = x2 – 4x + 4 – y2
* Lời giải:
– Ta có : A = x2 – 4x + 4 – y2 [để ý x2 – 4x + 4 có dạng hằng đẳng thức]
= (x2 – 4x + 4) – y2 [nhóm hạng tử]
= (x – 2)2 – y2 [xuất hiện đẳng thức số A2 – B2]
= (x – 2 – y )( x – 2 + y)
⇒ A = (x – 2 – y )( x – 2 + y)
Dạng 8: Tìm giá trị của x
Ví dụ: Tìm giá trị củ x biết: x2( x – 3) – 4x + 12 = 0
* Lời giải.
x2 (x – 3) – 4x + 12 = 0
⇔ x2 (x – 3) – 4(x – 3) = 0
⇔ (x – 3) (x2 – 4) = 0
⇔ (x – 3)(x – 2)(x + 2) = 0
⇔ (x – 3) = 0 hoặc (x – 2) = 0 hoặc (x + 2) = 0
⇔ x = 3 hoặc x = 2 hoặc x = –2
⇒ Kết luận, vậy nghiệm : x = 3; x = 2; x = –2
Bài viết liên quan:
![[ Kiến Thức Cơ Bản Về Bất Đẳng Thức ] lớp 8, lớp 9, lớp 10](https://thptchuyenlamson.vn/wp-content/uploads/2020/04/bat-dang-thuc-tam-giac.png) [ Kiến Thức Cơ Bản Về Bất Đẳng Thức ] lớp 8, lớp 9,…
[ Kiến Thức Cơ Bản Về Bất Đẳng Thức ] lớp 8, lớp 9,… Phương pháp phân tích đa thức dùng hằng đẳng thức và bài tập…
Phương pháp phân tích đa thức dùng hằng đẳng thức và bài tập…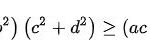 Bất đẳng thức bunhiacopxki là gì? Công thức tính…
Bất đẳng thức bunhiacopxki là gì? Công thức tính… Định Lý và Công thức Sin Cos Tan lớp 9, lớp 10, lớp…
Định Lý và Công thức Sin Cos Tan lớp 9, lớp 10, lớp…![[ Công Thức Lũy Thừa ] Của một tích, lớp 7 , lớp 12, bậc 3](https://thptchuyenlamson.vn/wp-content/uploads/2020/04/luy-thua-bac-3.png) [ Công Thức Lũy Thừa ] Của một tích, lớp 7 , lớp 12,…
[ Công Thức Lũy Thừa ] Của một tích, lớp 7 , lớp 12,… Các Công Thức Lượng Giác lớp 9, lớp 10, lớp 11 – Sin Cos…
Các Công Thức Lượng Giác lớp 9, lớp 10, lớp 11 – Sin Cos…
Tiết kiệm
![]()
![]()








